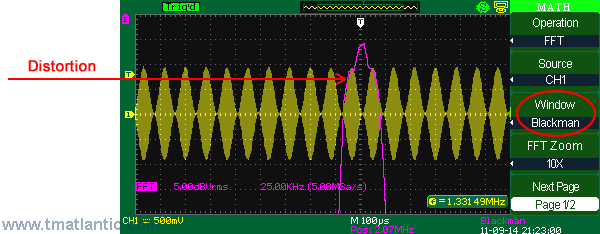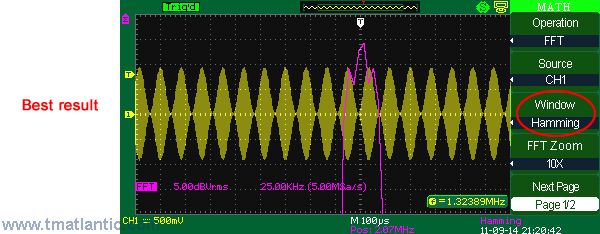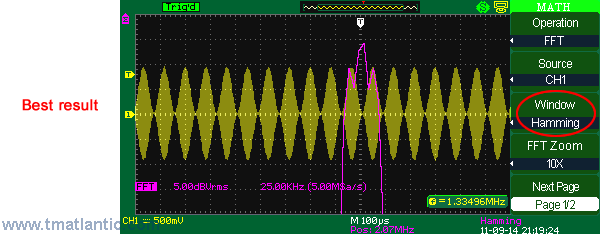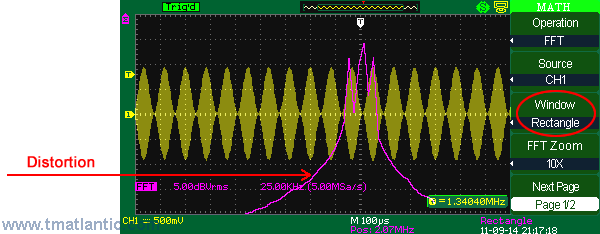
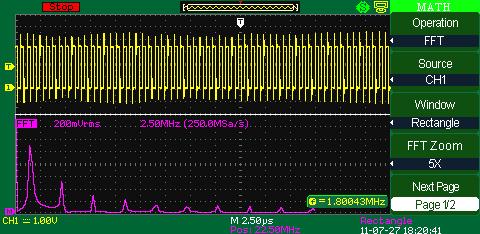
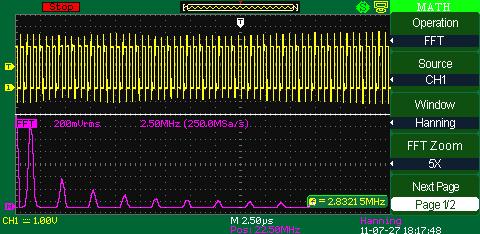
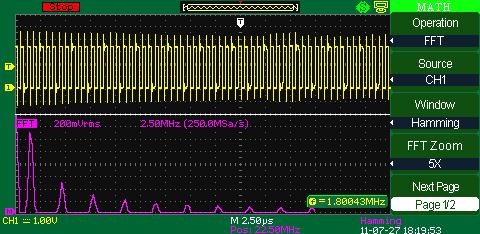
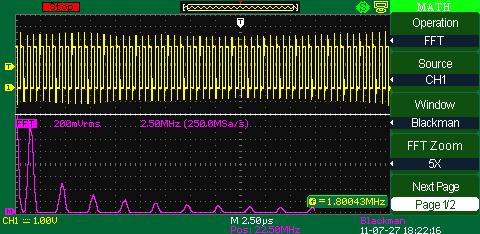
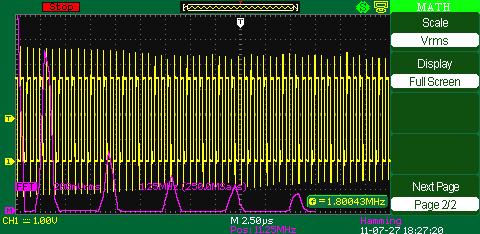
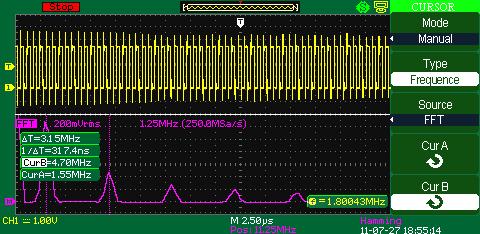
FFT (fast Fourier transform)

Fast Fourier transform (FFT) is a digital oscilloscope mathematical function which converts a time-domain signal into its frequency components mathematically namely performing signal spectral analysis.

FFT theory comes from the assumption of periodic signal and for the ideal transform it’s necessary to accurately mark one or several signal periods out what is impossible to do exactly for real signal. It can cause assumed function discontinuity, calculating frequency spectrum distortion (expansion).

FFT window function is used for the edge function suppression of real functions discontinuity by means of weight coefficient introduction for data access in the window which provides the edge points amplitude decay (start and stop) and therefore the FFT results improvement.

Different window function types (e.g. rectangle, Hamming, Hanning, Blackman–Harris) give different results both in precision and frequency resolution and they are used for different types of analyzed signals as well. Thus each of the window functions is a trade-off between the frequency resolution and amplitude determination accuracy. The right window function should be chosen depending on application field, signal source specifications and other parameters.

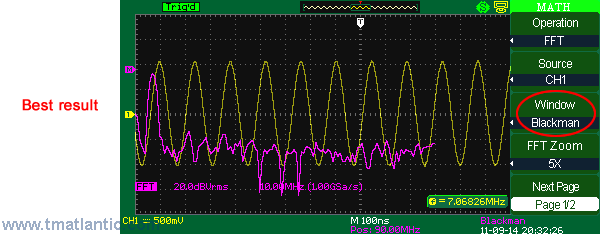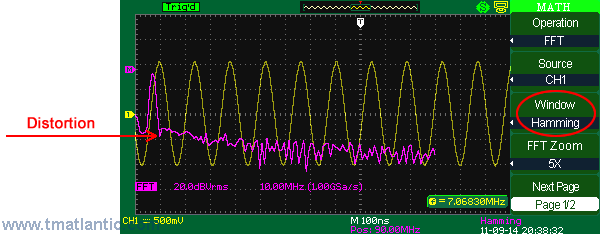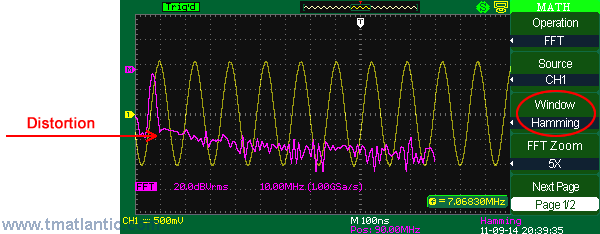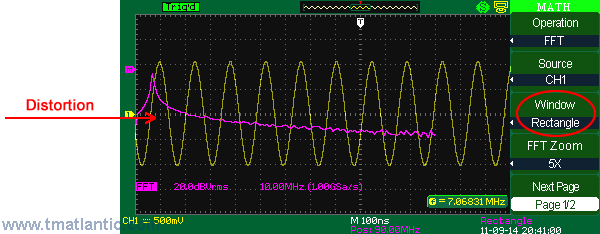
There are different window functions shown on the screenshots below used in Aktakom ADS-5302 digital oscilloscopes.

Rectangle.

The present window function realizes the best frequency resolution and the worst amplitude resolution. This is essentially the same as no window.

Hanning

Comparing to Rectangle it realizes better frequency resolution, but worse amplitude resolution.

Hamming

Hamming window function use leads to the frequency resolution better than in Hanning.

Blackman

Opposite to Rectangle Blackman provides the best amplitude resolution and the worst frequency resolution.

There are some additional means for more convenient viewing of FFT results available in Aktakom digital oscilloscopes. The most noticeable ones are the following:

• FFT results extension capability. The screenshots above show the use of quintuple zoom in FFT frequency domain.
• The capability to represent FFT results in two variants: in a double window (original signal – in the upper window, FFT results – in the lower one) or in a single window (both original signal and FFT results in one window). The screenshot of a single window is shown below

• Similar to mathematical functions there is colour signal differentiation used in FFT function. The original colour is yellow, FFT result is raspberry (red)
• Cursor measurement capability in frequency or amplitude domains with the measurement results displayed in a separate window on the screen.

In digital oscilloscopes FFT mode can be used in the following cases:

• harmonic components analysis in power networks;
• system harmonic components and distortion measurement;
• noise characteristic definition in DC voltage sources;
• filters and systems impulse response test;
• vibration and ripple analysis.

Also read about Pitfalls of Fast Fourier Transform.