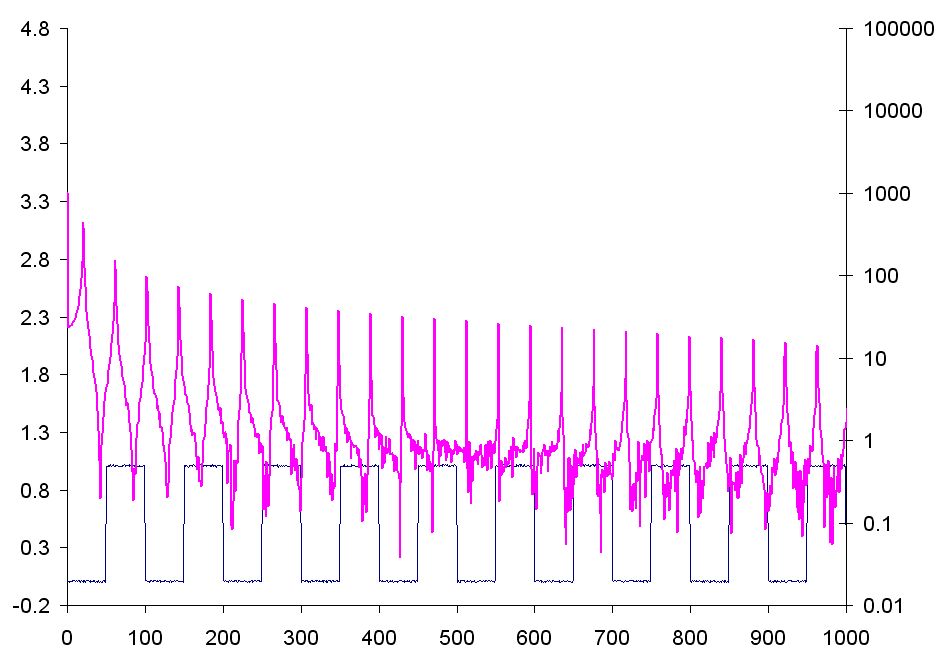
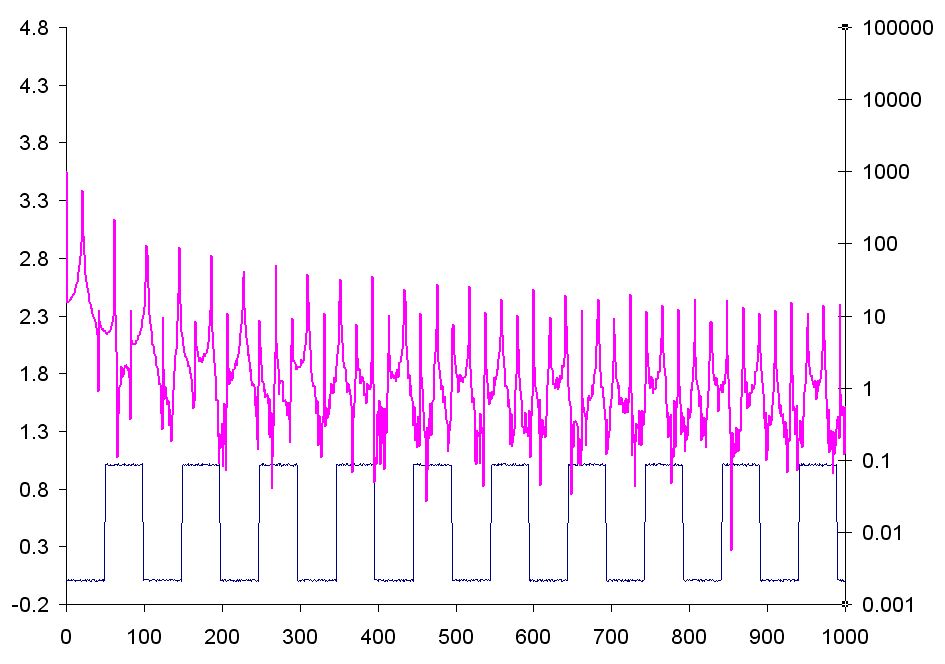
Pitfalls of Fast Fourier Transform

For spectral analysis of oscilloscope signals there is algorithm of Fast Fourier Transform (FFT) widely used. This fast and powerful tool gives opportunities to investigate the signal spectrum but unfortunately it also has its own disadvantages.

The main problem is the requirement to use strictly the signals of a certain length for FFT, and the signal length in the samples should be 2 raised to some power. It’s possible to make FFT with array of 1024 (512 or 2048) signal points but not of 1000 (500 or 2000) points. As a result a simple calibration signal of 1KHz frequency, shot on the sampling rate of 10 MHz, cannot be subject to FFT on its period length which will compose 1000 points in these terms. There can be two variants: you will have to use a bigger area for the analysis – 1.024 of the signal period (in that case the signal spectrum will be distorted, because FFT should be made exactly on the area of the signal period or the area multiple to it) or to make the oversampling of 1000-pointed signal to the virtual sampling rate of 10.24 MHz (in this case there is a possibility to distort waveform due to the interpolation used, that will also cause the signal spectrum distortion).

Another problem is the waveform discreteness. The signal can be measured in the certain points of time and the information about its condition in the intervals between these points is absent. As a result simple waveform instability across of ±1 sample, when the sampling rate is relatively low, can cause visual distortion. For example, on a oscilloscope display with the length of 1024 points there are 20-30 periods of the signal under investigation. That will correspond to 30-50 measurement points for one period, i.e. the error in 1-2 samples causes the error of FFT period of 2-7% which will be expressed in significant false artifacts on the spectrum image.

Therefore, in order to escape such FFT “reefs” it’s necessary to have a good understanding of the working process of this algorithm, carefully use it and to use the appropriate window functions if needed.

FFT result is the result of the edge conditions correctly aligned, i.e. signal area (inseparably periodic) and the window function suppressing the edge conditions imperfection (signal period noncoincidence with the transformation area).

False peaks are a sign of incorrect edge conditions, i.e. false frequencies introduced by the periodic function rupture.

You can make a simple experiment.

Set up FFT the best way on the sine signal displayed from the generator (signal period exactly coincides with FFT area) and then slowly change the external signal frequency. You will see that the more you move away from the ideal coincidence of the periods, in addition to the main harmonic peak shift, there appear complex spectrum peaks of edge conditions frequencies. Increasing in amplitude these peaks move backward from the main harmonic movement (because the function continuity is gradually worsening). At some point the false peaks get lots of satellites and become commensurate with the main signal harmonic.

The experiment described above can be made with TEKTRONIX DPO3000 and Aktakom ADS-2061M. It doesn’t depend on the device manufacturer but more on the user’s skills and understanding of FFT principles.

While studying the FFT transform opportunities (FFT) it’s necessary to take into account that synchronization accuracy in digital oscilloscope cannot be better than ±1 sample. It may seem that this mistake is insignificant, but its influence on FFT result can be seen on figures 1 and 2. As an example (common MS Excel with built-in analysis package was used) meander spectrum for waveform of 2048 points was calculated, on the figure 1 meander with period of 100 points is taken, on figure 2 - of 99 points. It can be easily seen that on the second waveform (99 points, fig. 2.) false peaks appeared in trenches between correct spectrum peaks, which are absent on figure 1.

With the help of special methods and preprocessing of the waveform more accurate FFT transform without false peaks (fig.2) can be achieved, but in many modern low cost digital oscilloscopes simple FFT algorithm without additional transform is used, and therefore false peaks can appear from time to time on the waveform displayed.