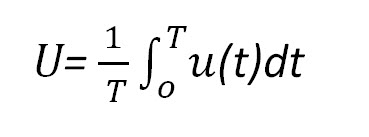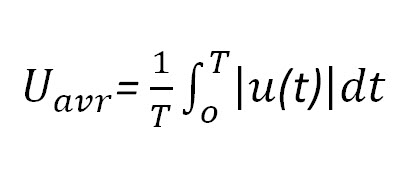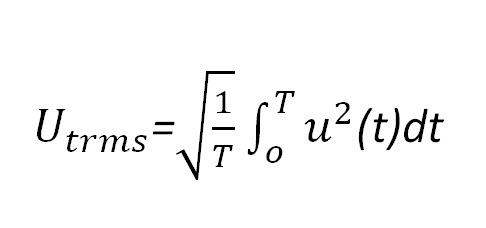Sinusoidal Voltage and Current Parameters

Alternating voltages and currents can be characterized by various indicators. For example, for an alternating periodic voltage of arbitrary shape u(t), in addition to the amplitude values, it can be characterized by:

average value (constant component)

average rectified value

effective or actual value

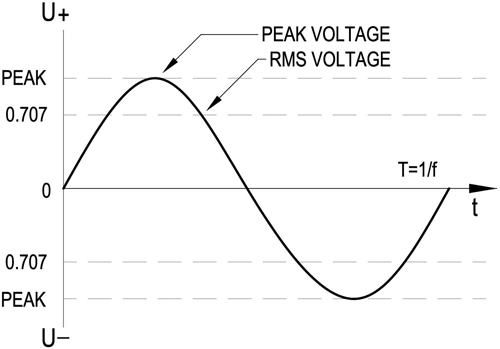
Most often, the effect of alternating voltage or current is judged by the average power over a period that heats up the active resistance R through which alternating current passes (or to which alternating voltage is applied). The heating process is inertial and usually its time is much longer than the period T of alternating voltage or current. In this regard, it is customary to use the effective value of sinusoidal voltage and current. In this case:

From here it is clear that to measure the effective value of a sinusoidal voltage or current, it is enough to measure their amplitude value and divide by √2 = 1.414 (or multiply by 0.707).

Figure 1

Typical relationships between voltage amplitude and effective value:

AC voltmeters and ammeters are often used to measure non-sinusoidal AC voltage and current levels. Theoretically, such signals can be represented by a Fourier series, consisting of the sum of the constant component of the signal, its first harmonic and the sum of higher harmonics. For linear circuits, due to the principle of superposition, the power of a non-sinusoidal signal is determined by the power of all its components. It depends on the harmonic composition of the signal, determined by the signal shape.

As a rule, regardless of the measurement method, they are usually calibrated in effective values of sinusoidal alternating voltage or current. Usually in this case, with the help of a full-wave rectifier, voltages or currents are rectified and it is possible to measure their average rectified voltage (often it is simply called average, but this is not entirely accurate - see above). The deviation of the AC voltage shape from the sinusoidal one is usually taken into account by the shape factor:

For a rectangular signal (meander) k_F=1, and for a sinusoidal signal k_F=π/2√2=1.1107. This difference causes a large difference in readings even in these simple cases.

Nowadays, personal computers, cell phones with pulse-mode transmitters, pulse and resonant voltage converters and power supplies, electric drives with adjustable speed and other equipment that consume currents in the form of short-term pulses or sinusoid segments are widely used. In this case, the root mean square value of the signals must take into account all harmonics of its spectrum. In this case, it is said to be true root mean square (True RMS or TRMS).

Unfortunately, when measuring voltages and currents with different time dependencies other than sinusoidal, big problems arise due to the violation of the relationships between the average rectified or amplitude values of the alternating voltage or current and their effective values. Conventional voltage and current meters with averaged readings in this case give an unacceptably large error, see Fig. A simplified measurement of the effective value of currents can sometimes lead to an underestimation of up to 50% of the true results.

Comparison of different types of measurement of varying voltages and currents
A user who does not know this may wonder why the fuse in a device with a current of 10 A regularly burns out, although according to the readings of an ammeter or a conventional multimeter, the current is an acceptable value of 10 A. If the curve of the measured voltage or current deviates from the ideal sinusoidal shape, refinement using a factor of 1.1107≈1.1 becomes unacceptable. For this reason, meters with averaged readings often give incorrect results when measuring currents in modern power networks. In this regard, instruments have been created that measure the truly True RMS value of alternating voltage and current of any form, which is determined by the heating of a linear resistor connected to the measured voltage.

To quickly determine the RMS voltage or peak voltage of a periodic AC waveform use our online RMS Voltage Calculator.